They may be the exclusives of the Boolean world, where typical rules of addition, subtraction and complementation may not hold true for them, but XOR gates are nonetheless important logic gates that form part of many important applications and circuits.
For example, you can find them in adder circuits, pseudo-random number (PRN) generator circuits, signal crossing circuits, sequence detection circuits and a lot of other circuits and devices.
This article will provide a quick review of the basics of XOR gates to help you dust off your knowledge of these all-too vital logic operators.
XOR Gates Basics
XOR gates (sometimes also referred to as Exclusive OR gates) are digital logic gates that have two or more inputs and one output and perform the function of exclusive disjunction.
What is the exclusive disjunction function?
The exclusive disjunction function is a logic operation that yields a true (HIGH) output only when an odd number of its inputs are true.
Applying this to a two input XOR logic gate:
The logic gate will produce a HIGH output if exactly one of its input is High;otherwise, it will produce a LOW output.
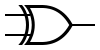
The truth table of a two-input XOR gate is as follows:
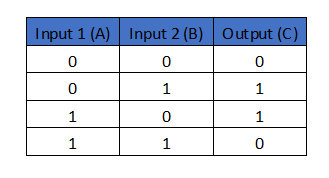
Translating the relationship between the inputs and outputs on the basis of the truth table drawn above, the Boolean expression for the logic gate can therefore be written as:
C = A’B + AB’
Since XOR logic gates don’t represent any traditional Boolean function, such as addition, multiplication or complementation, they need to be implemented using a combination of different basic logic gates connected together.
In case of a two-input XOR logic gate, the gate circuit can be designed using either a combination of:
- one OR gate and two AND gates; or
- four NAND gates
Thankfully, you don’t have to do that yourself, as there are pre-built XOR gate ICs available in the market. These ICs can help you add XOR gates in multiple configurations to your specialty product or system.